Elektrokémia – Elméleti összefoglaló
Elméleti összefoglaló
Az alábbi egyenlet összefoglalja Faraday I. és Faraday II. törvényét. Segítségével kiszámíthatjuk az adott elektródon leváló anyag tömegét m [g].
z: a félreakcióban az átadott elektronok sztöchiometriai együtthatója.
I: [A] az áramerősség,
t: [s] az eltel idő,
szorzatuk az eltelt idő alatt átadott töltésmennyiség Q: [C].
M [g/mol] a moláris tömeg,
F: [C/mol] a Faraday állandó.
Az utóbbi az elektron fajlagos töltését írja le, egy proton töltésének Q [C], és az Avogadro számnak NA [1/mol] a szorzataként. Az elektron töltése helyett a proton töltése az előjel miatt szerepel a képletben. A fenti egyenletben szereplő valamennyi változó kiszámítható a másik négy ismeretében. Fontos kiemelni, hogy csak addig érvényes az összefüggés amíg nem változik az áramerősség az idő függvényében.
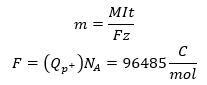
Ha elektródokon gáz fejlődik, ennek a térfogatát V [m3] is ki tudjuk számítani. Felírjuk az állapotegyenletet, és átrendezés után behelyettesítjük az anyagmennyiséget n [mol]. Az utóbbit az első egyenlet leegyszerűsítésével kaphatjuk meg. Az állapotegyenletben szereplő állandó analóg módon az Avogadro állandó és a Boltzmann állandó szorzata. A térfogatra kapott érték az anyagmennyiség és a moláris térfogat szorzataként is felírható. Hasonlóan a gáztér nyomásának Δp [Pa] a növekedését is megkaphatjuk, ha állandó annak térfogata.
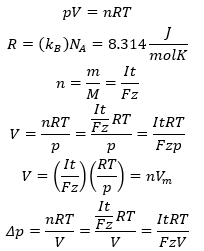
Ha az áramerősséget a felületre vonatkoztatjuk, egy új mennyiséget, az áramsűrűséget j [A/m2] kapjuk. Ez lokálisan jellemzi a folyamatot az elekród felületén. Ha ennek segítségével írjuk fel az egyenletet, a leváló szilárd anyag sűrűségével ρ [kg/m3] kifejezhetjük annak réteg vastagságát h [m].
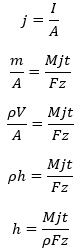
Egy telepnél az elektromotoros erő EME [V] megkapható az elektródok potenciáljának ε [V] a különbségéből. Egységnyi koncentrációk és standard körülmények között az elektródok potenciálja megegyezik a táblázatosan megadott standard elektród potenciálokkal ε0 [V].
![]()
Ismerve az elektromotoros erőt és az áramerősséget leíró egyenleteket, felmerülhetne, hogy teljesítményt P [W] számítsunk. Ez viszont helytelen lenne, mivel az elektromotoros erő csak akkor egyezik feszültséggel U [V], ha nem folyik áram a rendszerben.
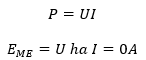
Áram alatt az elektródok polarizálódnak, vagyis a potenciál az áramerősség, pontosabban az áramsűrűség függvényében változik. Az ezt leíró összefüggések túlmutatnának a tananyagon. A korábbiak alapján csak annyit tudunk megállapítani, hogy ameddig nem folyik áram a rendszerben, addig az elektromos teljesítmény értéke is nulla lesz.
Itt érdekes elgondolkozni azon, hogy feszültséget nem lehet mérni áram nélkül. Ez alapján az elektromotoros erő nem lenne megmérhető. Gyakorlatban ezt nagyon nagy ellenállású műszerekkel oldják meg, vagy a kompenzáció elvét alkalmazzák. (Ez utóbbi esetben egy segédáramforrást egy csúsztatható ellenállással kötnek be, majd az ellánállás csuszkájára egy másik körbe kötik a vizsgálandó galvánelemet egy ampermérővel együtt. A csúszka helyzetét addig változtatják, amíg az ampermérő nem mutat áramot. Ebben az esetben a galvánelem körében nem folyik áram. A csúszka értékét leolvasva kiszámítható, hogy mekkora feszültség esik arra az ellenállás részre, amelyik a vizsgált galvánelemmel be van kötve. Ez az érték lesz a keresett elektromotoros erő.)
Nernst-egyenlet:
Ha a fenti feltételek nem teljesülnek, az elektród potenciálok standard értékét ε0 [V] a Nernst-egyenlet szerint korrigálhatjuk. Az új tagban az egyetemes gázállandó R [J/molK], hőmérséklet T [K] és a Faraday állandó F [C/mol] mellett a félreakcióban az átadott elektronok sztöchiometriai együtthatója z [] is szerepel. A logaritmus után a félreakcióban résztvevő anyagok koncentrációja alapján írjuk fel a tömeghatás törvényét. Az oxidált oldalon szereplő vegyületeknek a normalizált koncentrációját C [] szorozzuk, a sztöchiometriai együtthatókat a kitevőbe téve, ezt írjuk számlálóba. A normalizált mennyiség a koncentráció és az egységnyi koncentráció hányadosa. A logaritmus utáni tényezőknek dimenziómentesnek kell lennie. A redukált oldalon szereplő vegyületek esetén hasonlóképpen töltjük ki a nevezőt.
![]()
A Nerst egyenletet alább a redukció irányában felírt félreakció szerint írtuk fel a rendszerre. Itt a szabályosan felírt valamennyi együttható értéke egy, de ha az összeset végig szoroznánk egy adott n értékkel, a potenciál értéke akkor sem változna. A kapott új egyenletből eltűnik n, ha a logaritmus azonosságai szerint egyszerűsítünk.
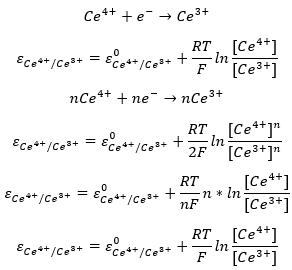
Gyakori, hogy valamelyik redoxi folyamatban szereplő vegyület nem az oldatban van, hanem szilárd fázisban. Az elektródok hajlamosak feszültség alá helyezve reakcióba lépni az oldatok komponenseivel. Ez alól általában kivétel a grafit és platina elektród, ezeket indifferens elektródoknak nevezzük. Ebben az esetben a szilárd fázisban lévő vegyület koncentrációja állandónak tekinthető. Ennek következtében nem kell, és nem is szabad beírni ezeknek normalizált koncentrációját az egyenletbe. Ezt a réz elektród példáján mutatjuk be. Ugyan ez vonatkozik a vízre, mivel híg oldatokban a koncentrációja állandó. Tömény oldatok esetén a Nerst egyenlet a felírt formájában nem használható pontosan.
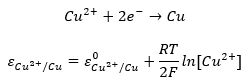
Az alábbi példa segítségével megvizsgálhatjuk, hogy a fenti állítás igaz. Írjuk fel az egyenletet helytelenül, és a standard potenciál helyett egy ε* tagot írjunk. Ha a második tagot a logaritmus azonosságai szerint felbontjuk, a szilárd fázisra vonatkozó része konstans lesz. Ez utóbbit összevonhatjuk ε* értékével, és összegük fogja adni a standard potenciált. Így visszajuthatunk a fenti egyenlethez.
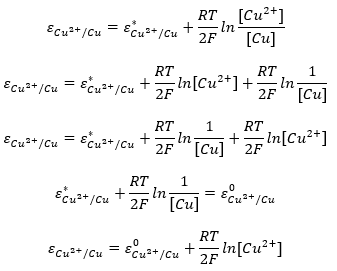
Amennyiben gáz komponens is szerepel az egyenletben, azt normalizált parciális nyomásban írjuk be a tömeghatás törvényének megfelelően. Ebben az estben 105 Pa nyomásra vonatkoztatunk, emiatt a normalizált mennyiségnek az értéke sem fog megegyezni az eredetivel.
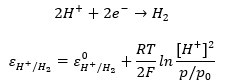
Belátható, hogy a hidrogén gáz parciális nyomásának a pontos beállítása problémás. A fenti elektród, melynek sztenderd potenciálja konvenció szerint nulla, nem könnyen kezelhető. Mivel a proton koncentráció szerepelt benne, alkalmas lehetne pH mérésre. A problémát megkerülhetjük, ha az alábbi szerves kémiai félreakciót alkalmazzuk. Ezt hívják kinon hidrokinon elektródnak. Mivel mindkét szerves vegyület mérsékelten oldódik vízben, koncentrációjuk állandó az oldatban. Az elektród potenciálja emiatt csak a hőmérséklet és a kémhatás függvénye lesz.
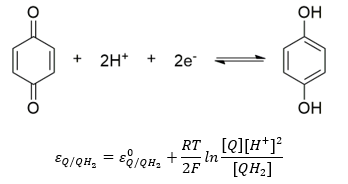
FEB-es feladat:
Számítsuk ki a Mn | MnSO4 || AgNO3 | Ag összeállítású galvánelem elektromotoros erejét!
[Mn2+] = 0,2 M [Ag+] = 0,3 M ε˚Ag/Ag+ = 0,80 V ε˚Mn/Mn2+ = – 1,05 V
Feladatok:
Középszintű érettségi feladatok
Emelt szintű érettségi feladatok
OKTV feladatok